Asish Mandoi

April 21, 2023⚬

A mathematical formulation using a simple logic of indexing the routes and finding an appropriate order of the route indices that leads to the optimal solution of the vehicle routing problem.

DWave's CQM (Constrained Quadratic Model) supports formulations with quadratic integer expressions in the constraints.

A general CQM expression cannot always be converted to a QUBO (Quadratic Unconstrained Binary Optimization), while the opposite can be done.

\text{QUBO} \subseteq \text{Constrained Quadratic Integer Optimization}

The following formulation of RAS, based on this more powerful class of problem formulation, has an advantage over other QUBO formulations requiring least number of variable definitions (potentially leading to a more efficient way of finding the solution).

VRP Definition

Given n clients and m vehicles (starting/ending at a depot), find routes for all vehicles to visit each client exactly once, minimizing total travel cost (predefined).

Inputs & Parameters

n: Number of clients (excluding depot).
m: Number of vehicles.
cost: 2D array with travel costs/distances from node i to node j (including the depot at index 0).
xc, yc: X and Y coordinates of all nodes (for visualization only).

Decision Variables

Routing (Edge) Variables

x[i][j]: (Boolean) 1 if there is an edge (route) from node i to node j, 0 otherwise.
Client-Vehicle Assignment Variables

y[i][k]: (Boolean) 1 if client i is visited by vehicle k, 0 otherwise.
Sequencing Variables

t[i]: (Integer) Sequence/order in which client i is visited (time at which any vehicle visits client i)

Constants

B: A relatively large constant for subtour elimination (B = 2n).

Objective

minimize(sum(cost[i][j] * x[i][j] for all i != j))

\text{min}\left(\sum_{i \neq j} C_{ij} \cdot x_{ij}\right)

Constraints

Routing Constraints

# Each client must have exactly one outgoing and one incoming edge

sum(x[i][j] for j != i) == 1      # Outgoing from client i
sum(x[j][i] for j != i) == 1      # Incoming to client i

\sum_{j \neq i} x_{ij} = 1

\sum_{j \neq i} x_{ji} = 1

# Each client must be visited by exactly one vehicle

sum(y[i][k] for k in 1..m) == 1

\sum_{k=1}^{m} y_{ik} = 1

# m vehicles leave and return to the depot

sum(x[0][i] for i=1..n) == m     # Leave depot
sum(x[i][0] for i=1..n) == m     # Return to depot

\sum_{i=1}^{n} x_{0i} = m

\sum_{i=1}^{n} x_{i0} = m

Client-Vehicle Assignment Consistency

# If there is an edge from i to j, both must be visited by the same vehicle

y[i][k] - y[j][k] + (1 - x[i][j]) >= 0
y[j][k] - y[i][k] + (1 - x[i][j]) >= 0
# For all i != j, k=1..m

\begin{array}{l} y_{ik} \ge y_{jk} - (1 - x_{ij}) \\ y_{jk} \ge y_{ik} - (1 - x_{ij}) \end{array} \quad \forall i \neq j,\, k \in \{1, \ldots, m\}

Subtour Elimination (MTZ Constraints)

Miller-Tucker-Zemlin constraints to prevent subtours (cycles that do not include the depot), using the sequence variable t.
Key constraints enforce ordering and proper sequencing, ensuring each tour is a single loop including the depot, not small disconnected loops.

# if vehicle k goes from i to j, then j must be visited after i

t[j] * y[j][k] - (t[i] + 1) * y[i][k] + B*(1 - x[i][j]) >= 0
# For all i != j, k=1..m

t_j y_{jk} \ge (t_i + 1)y_{ik} - B(1 - x_{ij}) \quad \forall i \neq j, k \in \{1, \ldots, m\}

NOTE

Think about when such a scenario is possible! Find a solution that satisfies all constraints except the Subtour Elimination Constraint.

VRP - 6 clients, 2 vehicles
Expected Solution	Unexpected Scenario

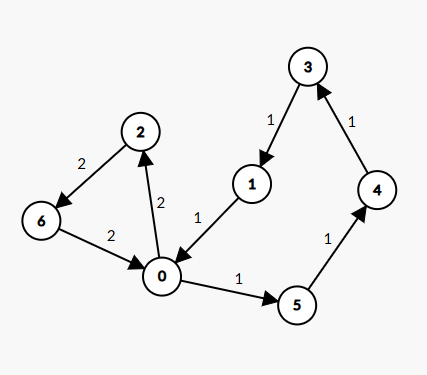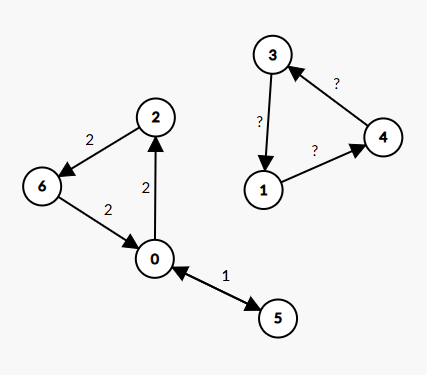Qubit Complexity

Order of number of binary variables required to represent the formulation: $O(n^2) \quad (\text{assuming} \quad m < n)$

Solution Process

The model is formulated with the above variables, objective, and constraints.
It is submitted to a hybrid quantum-classical solver (D-Wave's LeapHybridCQMSampler).
The solver returns multiple samples; only those that are feasible (satisfy all constraints) are considered.
If feasible solutions exist, the solution with the lowest cost (energy) is selected and reported.

Visualization

After solving, routes are visualized using the python libraries matplotlib and networkx:

Nodes represent depot and clients.
Edges represent routes taken by each vehicle (distinct colors).
Node and edge assignments are extracted from the best solution.

References

VRP Explorations by @Asish and others.

Route Activation Solver with DWave's CQM